PKoffee Analysis example

Welcome to the PKoffee project analysis notebook! ☕️

This project aims to analyze the relationship between coffee consumption (in cups) and productivity. We use several mathematical models to find the best fit for our data.

Project Structure

• pkoffee/data.py: Data loading and cleaning.

• pkoffee/parametric_function.py: Definition of various models (Quadratic, Logistic, etc.).

• pkoffee/productivity_analysis.py: Logic to fit models and rank them.

• pkoffee/visualization.py: Utilities to plot results.

import sys
from pathlib import Path
import os
from pkoffee.data import load_csv
from pkoffee.productivity_analysis import fit_all_models, format_model_rankings
from pkoffee.visualization import plot_models, Show

1. Load the data

The experimental data are in file ../analysis/coffee_productivity.csv

# Load the data
data_path = Path("../analysis/coffee_productivity.csv")
data = load_csv(data_path)

print(f"Loaded {len(data)} data points from {data_path}")
data.head()

Loaded 200000 data points from ../analysis/coffee_productivity.csv

	cups	productivity
0	9	0.424316
1	8	0.589516
2	9	0.397615
3	10	0.256125
4	10	0.255150

2. Model Fitting

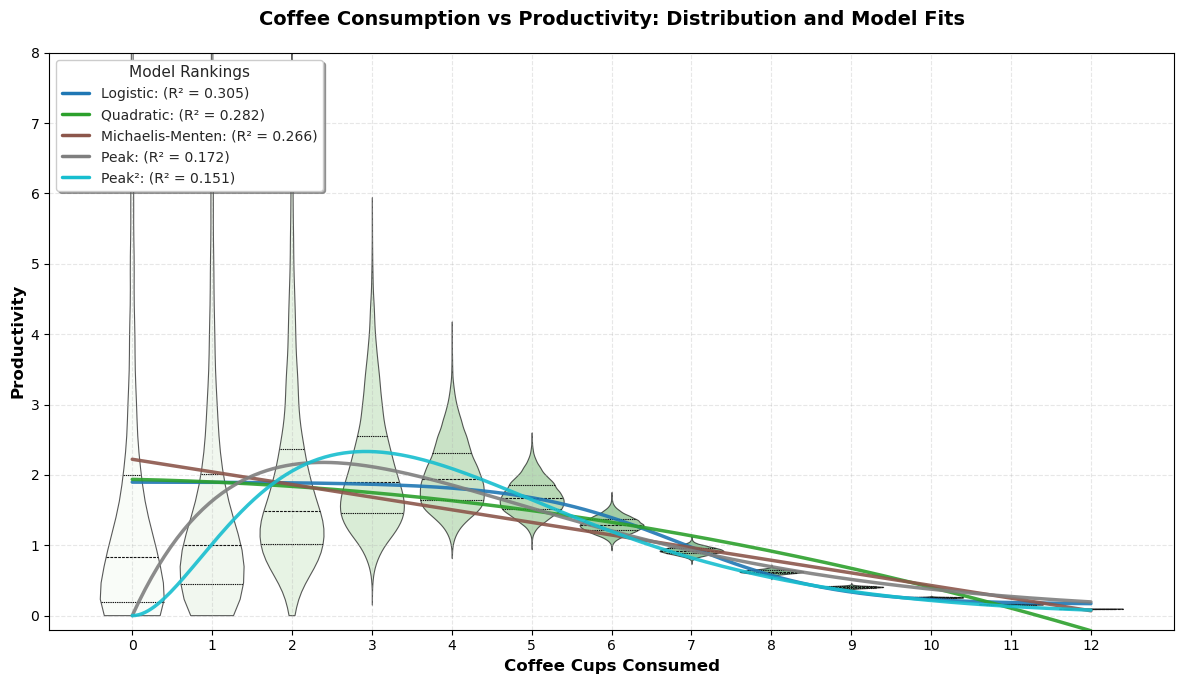
We will now fit several parametric models to the data:

• Quadratic: \(f(x) = a_0 + a_1 x + a_2 x^2\)

• Michaelis-Menten: \(f(x) = y_0 + V_{max} \frac{x}{K + x}\)

• Logistic: \(f(x) = y_0 + \frac{L}{1 + e^{-k(x - x_0)}}\)

• Peak Model: \(f(x) = a \cdot x \cdot e^{-x/b}\)

The fit_all_models function will run the optimization for all these models and rank them using the \(R^2\) score.

# Fit all models
fitted_models = fit_all_models(data)

# Print rankings
print("Model Rankings (by R²):")
print(format_model_rankings(fitted_models))

Model Rankings (by R²):
Model Rankings:
══════════════════════════════════════════════════
Rank   Model                R² Score
══════════════════════════════════════════════════
1      Logistic             0.3051
2      Quadratic            0.2815
3      Michaelis-Menten     0.2662
4      Peak                 0.1724
5      Peak²                0.1511
══════════════════════════════════════════════════

3. Visualization

Finally, we visualize the data distribution using a violin plot and overlay the fitted model curves to see which one accurately captures the “coffee sweet spot”.

plot_models(data, fitted_models, show=Show.YES)